Analizando los sueldos de la industria del software en Argentina (Parte 2)
En el primer post hicimos un análisis exploratorio general de los sueldos, en este vamos a realizar una inferencia estadística. Otra vez, todo el código se encuentra disponible acá.
Hipótesis
Primero formulamos una hipótesis:
Los salarios varían significativamente según el género
Para probar nuestra hipótesis, intentaremos refutar la hipótesis nula, que simplemente sería lo contrario (los salarios no varían según el género)
Primer problema: los tamaños de las muestras
Recordemos la distribución de salarios discriminada por género:

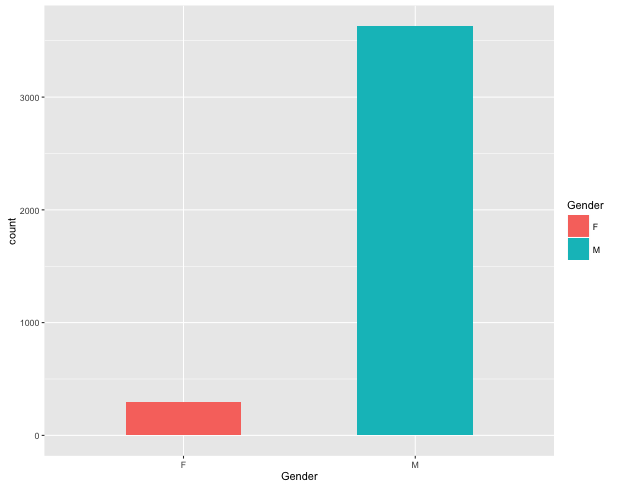
El problema en este caso es la diferencia entre participantes de la encuesta varones y mujeres. Usemos un gráfico de barras para hacerlo más evidente:

Hay 298 mujeres y 3.631 hombres en nuestro dataset. Si consideramos a la muestra como representativa de la población, habría aproximadamente una mujer cada 10 hombres, o un 7.5% del total de trabajadores de software.
Con esta limitación en mente, vamos a tratar de poner a prueba nuestra hipótesis utilizando 3 estrategias alternativas.
Usar muestras de tamaño comparable
Sería muy bueno tener misma cantidad de mujeres que de hombres. Una alternativa sería salir a encuestar más mujeres. La otra (más fácil) es “recortar” la muestra de varones.
Para esta última tomamos una muestra aleatoria de 298 varones de nuestros datos y comparamos las dos. Vamos a usar una función del histograma de ggplot llamada “dodge” para que no apile las barras sino que las ponga una al lado de la otra:

Si bien parece haber mayor cantidad de mujeres en los deciles más bajos, a simple vista las distribuciones no muestran una diferencia importante que nos sugiera descartar la hipótesis nula.
Comparar las áreas de las distribuciones
Otra forma de salvar el problema de las cantidades es utilizar un gráfico de densidad de área. Este tipo de gráfico no compara unidades absolutas sino que estima porcentaje de muestras bajo la curva (para más información, la técnica que usa ggplot para esto se llama Kernel Density Estimation o KDE).
Probemos la técnica generando una distribución normal aleatoria, usando la función rnorm:

Vemos una campana de Gauss casi perfecta, en este caso con una media de 5 y una desviación estándar de 2. Nótese que no importa la cantidad de elementos, el eje Y no presenta cantidades sino porcentajes. En este caso el gráfico se hizo con 5.000 elementos pero uno de 50.000 mostraría un área similar.
Grafiquemos las curvas estimadas de densidad para varones y mujeres, usando esta vez la totalidad de los datos:

Las curvas de densidad son similares. Este gráfico tampoco hace evidente una diferencia entre las medias. Vamos al tercer paso.
ANOVA
Para finalizar vamos a usar una herramienta llamada ANOVA o Analysis of Variance. La técnica se utiliza para comparar medias de distribuciones y determinar si la variación entre esas medias puede ser explicada por el azar.
Con R esto es muy sencillo, se arma un modelo lineal y se calcula el anova con la función homónima:
> model <- lm(Income ~ Gender, data=clean) > anova(model)
Analysis of Variance Table
Response: Income
Df Sum Sq Mean Sq F value Pr(>F)
Gender 1 1.8123e+09 1812255174 9.5573 0.002006 **
Residuals 3927 7.4464e+11 189620819
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1De toda la información que R nos devuelve, nos interesa el Pr(>F) que en este caso es 0.002. Este número es la probabilidad de observar estos resultados si las distribuciones de salarios por género fueran iguales.
Esto es significativo.
Lo que ANOVA nos dice es que, suponiendo que la distribución de salario es independiente del género, la probabilidad de encontrar una muestra con esta diferencia salarial entre géneros es del 0.2%, dicho de otra manera una en quinientos.
Podemos decir entonces que es muy poco probable que se deba al azar y concluir, por tanto, que las distribuciones no son iguales.
Conclusión
Pudimos descartar nuestra hipótesis nula. Descubrimos que efectivamente las mujeres cobran menos que los hombres en la industria. Como vimos a lo largo de este proceso, a veces esto no es evidente y requiere probar distintas fórmulas o estrategias para corroborar nuestra hipótesis.
Saludos!
Gracias a: Nadia Kazlauskas, Mauro García Aurelio, Román Avila, Alejandro Crosa, Andrés de Barbará, Mariano Barrios